顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k（a≠0，k为常数）顶点坐标：-b/2a，[（4ac-b）/4a]。知道了二次函数的顶点坐标公式，就可以直接计算出给定二次函数的顶点坐标。

二次函数的顶点坐标公式

二次函数的顶点坐标公式是一个非常重要的数学工具，它可以帮助我们快速找到二次函数的最大值或最小值（取决于二次函数的开口方向）。

对于一般的二次函数y=ax2+bx+c（其中a=0），其顶点坐标公式为：

x顶点=b/2a

y顶点=（4ac-b）/4a

或者，顶点坐标也可以表示为：-b/2a，[（4ac-b）/4a]

这个公式的推导过程涉及到二次函数的配方。具体来说，我们可以将二次函数y=ax2+bx+c改写为顶点式：

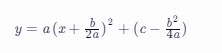
这样，我们就可以直接读出顶点坐标为-b/2a，[（4ac-b）/4a]

需要注意的是，当a>0时，二次函数开口向上，顶点为最小值点；当a<0时，二次函数开口向下，顶点为最大值点。

此外，如果二次函数已经是以顶点式y=a(xh)2+k给出的，，那么顶点坐标就是(h,k)。

总的来说，二次函数的顶点坐标公式是一个非常实用的工具，它可以帮助我们快速找到二次函数的极值点，进而分析二次函数的性质。

二次函数的顶点坐标公式如何应用

二次函数的顶点坐标公式为(-b/2a, (4ac-b)/4a)。 这个公式可以用来直接计算出二次函数图像的顶点坐标。其中，-b/2a是顶点的x坐标，表示对称轴上的点;(4ac-b)/4a是顶点的y坐标，表示抛物线的最高点或最低点。

具体应用步骤如下：

确定系数：首先，需要确定二次函数的一般式y=ax+bx+c中的系数a、b和c。

应用公式：将系数代入顶点坐标公式(-b/2a, (4ac-b)/4a)，计算出顶点的坐标。

分析结果：根据计算出的顶点坐标，可以分析抛物线的开口方向、顶点位置等信息。例如，当a>0时，抛物线开口向上;当a<0时，抛物线开口向下。例如，对于二次函数y=2x-4x+1，可以按照以下步骤应用顶点坐标公式：

确定系数：a=2，b=-4，c=1。

应用公式：顶点坐标为(-(-4)/(22), (421-(-4))/(42)) = (1, -1)。

分析结果：抛物线的顶点坐标为(1, -1)，开口向上，因为a>0。