因为按照似然函数的思路，相比于“琳达是一名银行出纳”的论断，“琳达是一名银行出纳，并且积极参加女权运动”的论断，更可能得到琳达关心歧视和社会公正问题等具体描述。而没有注意到，对于后验概率，还需要关注先验概率prior，而f选项的prior明显比h大得多。

类似的认知谬误比比皆是，我们可以再看赌徒谬误的例子，里面混淆了前提假设和后验概率。

赌徒谬误[3]说的是：

抛一枚公平的硬币，连续出现越多次正面朝上，下次抛出正面的机率就越小，抛出反面的机率就越大。

把这个谬误和热手谬误[4]及选择性记忆相结合，就不难理解为何赌徒永远赢不了。理性的分析容易看到，每次抛硬币都是相互独立事件，前面的结果不会对之后的结果产生影响。而我们又有了前提假设：硬币是无偏的。所以不管哪次抛掷硬币，出现正反的可能性都是1/2。

更精确的，我们可以用数学语言描述。假设硬币出现正面朝上的概率为h,已抛掷4次，每次都是正面朝上，这一事实表述为O. 硬币无偏，满足P(h=0.5)=1,则下一次出现正面朝上的概率为P(u,O|h=0.5)=0.5，出现反面朝上的概率也是P(d,O|h=0.5)=0.5.

但是，赌徒错误的使用了硬币无偏的结论，没有把它看成是前提假设，而看成是证据之后的推断，也就是后验概率。因为之前四次的正面朝上已经让硬币正面朝上的概率偏向于E(h)>0.5,为了维持硬币无偏的信念，那么我们期望的是下次的抛掷能使E(h)偏回来一点。

具体的，我们假设h的先验分布是均匀的（当然这里只是为了方便，用其他的分布不影响结论），那么抛掷四次正面朝上，使我们对h的概率预期变为：

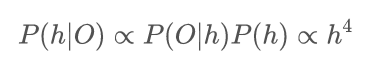
可以得到期望E(h|O)=5/6。和设想的一样，经过四次正面朝上后，我们的证据偏向于硬币是h>0.5的。然后我们计算，下一次抛掷结果分别为正面朝上u和反面朝上d，h后验概率的期望。具体的：

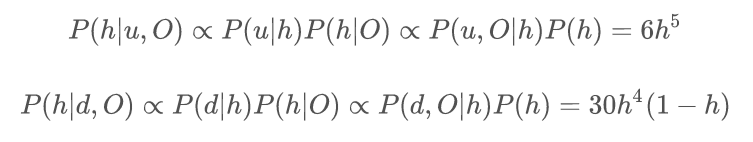
由此，计算可得E(h|u,O)=6/7,而E(h|d,O)=5/7.可以看到，确实下一次抛掷如果反面朝上便可以增强我们对硬币无偏的信念。不仅如此，我们还可以发现E(h|O)介于两者之间。

总结

我歌月徘徊，我舞影零乱。我们的贝叶斯大脑根据已有知识对外界进行响应。这一方面让我们可以在稀疏的、少量的、只有正例的情境下快速学习、构建各种概念。但同时，也得警惕这种启发式的学习可能导致的各种认知谬误。

更多阅读

参考文献：

[1]: Murphy, K. P. (2012).Machine Learning: A Probabilistic Perspective(1 edition). Cambridge, MA: The MIT Press.

[2]: Xu, F., & Tenenbaum, J. B. (2007). Word learning as Bayesian inference.Psychological Review,114(2), 245.

[3]: [维基百科：赌徒谬误](https://zh.wikipedia.org/wiki/%E8%B3%AD%E5%BE%92%E8%AC%AC%E8%AA%A4)

[4]: 热手谬误认为某事多次发生则未来发生的机率会较大，见维基百科。