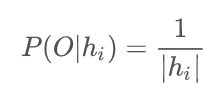
所以我们可以看到，因为满足“都是4的幂次”假设的结果只有4,16,64三种，所以16对应的似然概率为1/3。

根据贝叶斯定理，最终对每种假设的信念便是两者的乘积，既要考虑到先验假设，也要考虑到似然概率，相乘的结果显示在图中横坐标为“post"的右侧。对于”都是偶数“这样的假设，尽管先验概率比较大，但因为1到100间的偶数太多，出现16的概率仅1/50，如果恰恰出现了，我们会觉得是“惊人的巧合”，而不太会相信它是真的。这对应着贝叶斯版的Occam剃刀，在机器学习中，它化身为正则化项以防止模型过拟合。

这样，我们就有了知道数字16后各模型的后验概率P(h_i|O),从中我们就可以选择概率最大的一个作为最大似然估计，图中，我们可以看到选出的模型是“都是4的幂次”。如果有更多的证据，模型便会快速收敛至真实情况。

那么我们又是如何猜测下一个数字x的呢？我们已经有了每个模型的后验概率，下一个数字是x的概率就可以表示为每个模型的后验概率和相应模型出现x的概率的乘积的求和，俗称贝叶斯模型平均。表示为：

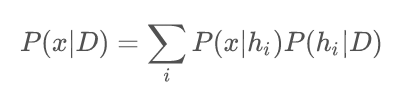
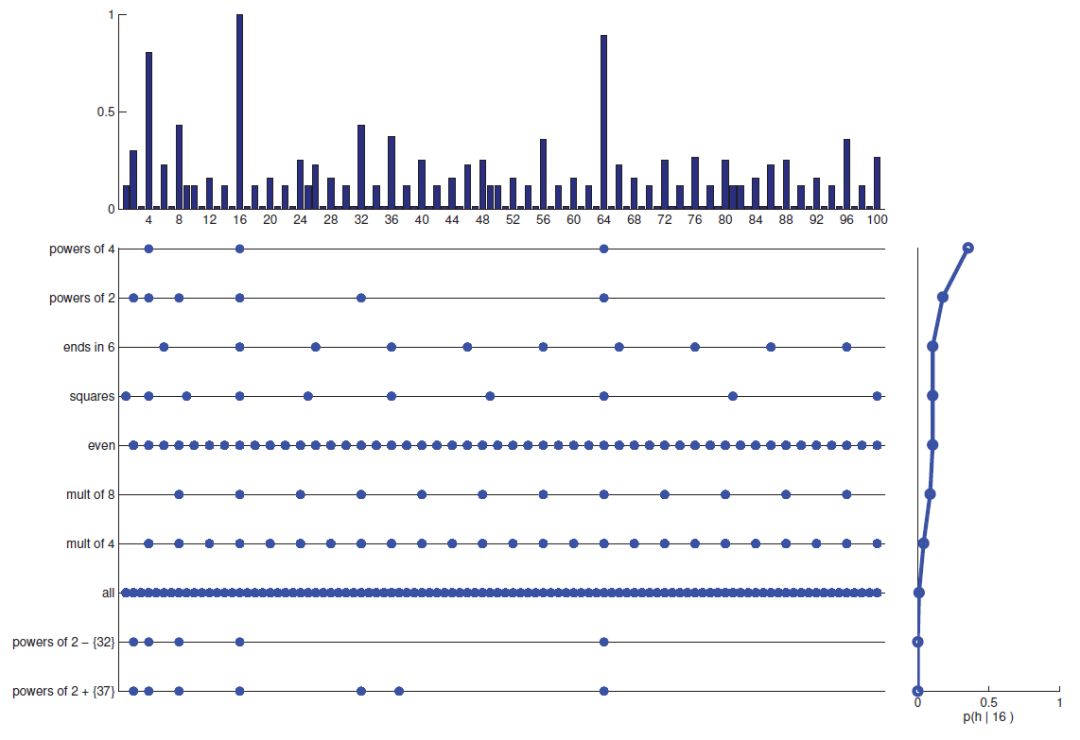
这一计算过程漂亮的反映在上图中。中间那一大块图纵轴表示各种可能假设，而每条横线表示1到100的数值区间，那么每条线上的点便表示各模型假设允许出现的数值。可以看到假设“all"的横线布满了点，因为从1到100，它每个数都可以取到。我们再看图的右边那条曲线，它表示的便是给定数值16后各模型的后验概率分布，可以看到，假设”都是4的幂次“的后验概率最大。将两者结合并叠加起来，就会得到图中上部所示的x的概率分布。可以看到，数字16,64,4的概率最大，与我们料想的非常一致。

我们再看大脑推断中用到贝叶斯的两个例子。第一个例子同样来自Tenenbaum[2]的论文，说的不仅仅是我们如何学习单个概念，还说明了我们是如何将概念对应到事物的不同范畴的。所谓范畴，就是对事物的分类，并且这种分类通常是有不同层次的。例如你的写字桌，它既属于写字桌这一类，也属于桌子这一类，还属于家具这一类，在范畴论中，它分别可以对应着下位范畴、基本范畴和上位范畴。

在Tenenbaum论文的例子中，当指着一张标记为fep的斑点狗图片，来猜测fep的含义时，我们既可以认为fep表示上位范畴的动物，表示基本范畴的狗，也可以是表示下位范畴的斑点狗。而我们会倾向于推断fep的意思是狗。这是由基本范畴偏差（prior)造成的，因为我们日常处理事物大多都在基本范畴，这也是为什么基本范畴的中英文单词大多非常简单且长度很短。但当给了三张斑点狗的图片，而且每张都标记为fep的时候，我们却更可能推断fep意思是斑点狗而不是所有的狗。因为直观上来讲，如果fep表示的是所有的狗，但随机抽取的三个样本都是斑点狗，那将是“惊人的巧合”。

第二个例子来自刘未鹏的《暗时间》，里面提到了一个自然语言的二义性例子。

the girl saw the boy with a telescope.

对于上面这句话，我们既可以理解为那个女孩拿着望远镜看那个男孩，也可以理解为那个女孩看到那个拿着望远镜的男孩。那么为什么通常情况下，我们会想当然的理解为第一个意思而消除歧义？从语法结构上讲，两种结构都是成立的，在这里体现为先验概率P(h)大致一样，但是P(O|h)却很不一样。如果是第二种情况，那么为何偏偏那个男孩拿的是一个望远镜，而不是一本书或一只苹果呢？有很多不同的可能性，恰巧是望远镜的可能性是非常小的。但是如果用第一种语义理解就不一样了，女孩通过某种东西看男孩，那么，拿的是望远镜就很显然。

在很多情况下，贝叶斯原理很好用，我们大脑也用它做很多事。但另一方面，它也是认知偏差的孵化池。

认知偏差

在《机器人叛乱》一书中，斯坦诺维奇讲到了认知心理学文献中的琳达问题：

琳达今年31岁，单身、率真、非常聪明。她的专业是哲学。作为一个学生，她格外关心歧视和社会公正问题，也曾参加过反核示威游行。请根据可能性对下面的陈述进行评价，1代表可能性最高，8代表可能性最低。

a. 琳达是一名小学老师。

b. 琳达在书店工作，上瑜伽课。

c. 琳达积极参加女权运动。

d. 琳达是一名精神病学的社工。

e. 琳达是妇女选民联盟的一员。

f. 琳达是一名银行出纳。

g. 琳达是一名保险销售员。

h. 琳达是一名银行出纳，积极参加女权运动。

因为选项h是选项c和f的组合，所以从概率来看，肯定比两者来得小，但是研究表明，有85%的参与者出现了“组合偏差”，他们认为选项h比f的可能性更高。

这可以看成是混淆了似然概率与后验概率的区别。本来需要计算后验概率P(h|O)，却计算了似然函数P(O|h)，或者说本来需要用induction的地方却错误的使用了deduction。