买

高

中

低

不买

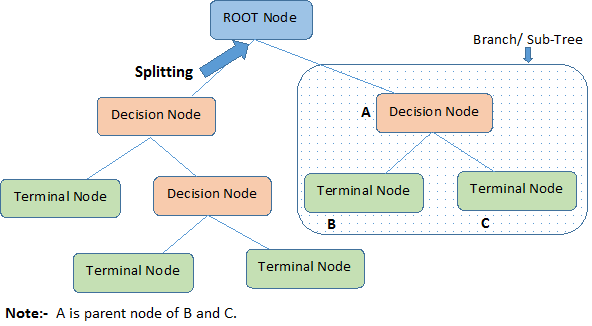
在一棵决策树上，其中的节点可以分成根节点（蓝色） 决策节点（红色）和终止节点（绿色），而图中的方框里包含的即是一颗子树，这么看来，树模型是不是特别好理解？树模型的第二个好处是可以方便的探索数据中那些维度更加重要（对做出正确的预测贡献更大），比如上述的买电脑的例子，你会发现对于大多数人来说，CPU的型号最关键。树模型的第三个好处是不怎么需要做数据清洗和补全，还用买电脑的例子，假设你拿到的数据部分中没有告诉GPU的型号，你不必要丢掉这部分数据，进入到相应的子树里，随机的让这条数据进入一个终止节点就好了，这样，你便能够利用缺失的数据了。

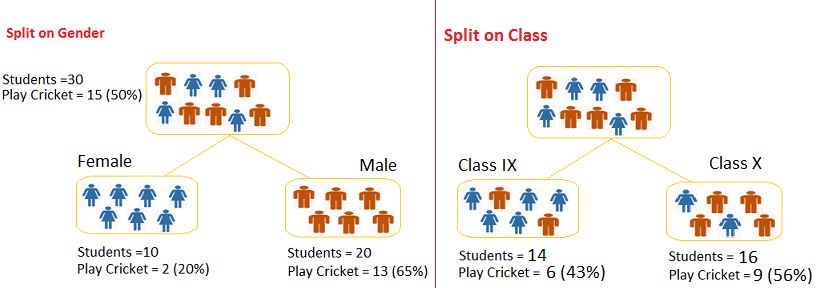
谈起树模型，就要说起基尼系数，这个指数最常见的场景是描述贫富差距，但也可以用来指导树模型在那里分叉。假设一颗最简单做二分类问题的决策树，拿到的数据分为两种特征，一个是性别，一个是班级，预测学生们愿不愿打板球，下面的图是两种不同的树模型，用性别来分，10个女生中有2个愿意打球，而20个男生中有13个愿意打球，而用班级分，效果则没有那么好，具体怎么计算了，先从左到右依次计算每个终止节点的基尼系数，(0.2)*(0.2)+(0.8)*(0.8)=0.68(0.65)*(0.65)+(0.35)*(0.35)=0.55(0.43)*(0.43)+(0.57)*(0.57)=0.51(0.56)*(0.56)+(0.44)*(0.44)=0.51，之后对每棵树的基尼系数进行加权平均 ：10/30)*0.68+(20/30)*0.55 =0.59（按性别分），(14/30)*0.51+(16/30)*0.51 =0.51（按班级分），因此在该例子中，性别是一个更好的特征。

理解决策树的下一个重要的概念是信息增益，信息可以看成是减少了多少系统中的无序，而描述系统的无序程度，可以用信息熵，对于二分类问题，计算公式是。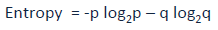

对于每一次树上的分叉，先算下父节点的熵，再计算下子节点的熵的加权平均，就可以计算出决策树中的一个决策节点带来了多少信息增益了。

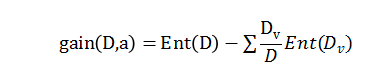
信息熵公式告诉我们的是，我们每次对所有特征都扫描一遍，选择那个让我们的信息增长最大的特征。 依次在这个特征的每个可能取值下，我们在寻找第二个关键特征，列出第二个特征选的可能取值并寻找第三个特征依次类推。 再对每一分支的操作里， 如果我们发现在某个特征组合下的样本均为一类， 则停止分叉的过程。 整个操作过程形似寻找一颗不断分叉的树木， 故名决策树。

决策树能够处理特征之间的互相影响， 因为特征之间的互相影响，我们并不像简单贝叶斯那样并列的处理这些特征。 例如某个特征可能在某个条件下式好的， 但在另外条件下就是坏的或者没影响。 比如说找对象，你只在对方漂亮的时候才care他学历。 我会根据之前问过的问题的答案来选择下一步问什么样的问题， 如此， 我就能很好的处理特征之间的关联。

我们把这样的思维步骤写成伪代码， 大概是这样的 :

训练集D（x1，y1）….

属性Aattribute（a1，a2…..）

函数treegenerate

1, 生成结点nodeA（任选一个特征）

2， 判断D在A中样本是否都属于类型C，是则A标记为C类叶结点， 结束

3， 判断A为空或D在A样本取值同（x相同而非y），将node标记为样本多数分类的叶结点（maxnumbers），结束

终止条件不成立则:

从A中选择最优划分属性a*,

循环:

对A*上的每一个值a*做如下处理：

If a*上的样本为空，则a*为叶节点 （该值下用于判断的样本不足，判定为A*中样本最多的类），

如果支点上的样本集为D**

如果存在某个位置，使得D**为空，

则A*为叶节点，

否则，以a*为分支节点，回到第一句